所以你知道贝叶斯规则。它与机器学习有什么关系?很难理解这些拼图是如何组合在一起的——我们知道这花了我们一段时间。这篇文章是我们当时希望有的介绍。
虽然我们对此事有所了解,但我们不是专家,因此以下内容可能包含不准确甚至完全错误的内容。随时在评论中或私下指出它们。
贝叶斯学派和频率学派
本质上,贝叶斯意味着概率。之所以存在特定术语,是因为概率有两种方法。贝叶斯主义者将其视为信念的度量,因此概率是主观的,指的是未来。
频率论者有不同的观点:他们使用概率来指代过去的事件——这样它是客观的,不依赖于一个人的信念。这个名字来自方法 - 例如:我们抛硬币 100 次,它出现了 53 次正面,所以正面的频率/概率是 0.53。
有关此主题及更多内容的深入调查,请参阅 Jake VanderPlas 的频率论和贝叶斯论系列文章。
先验、更新和后验
作为贝叶斯主义者,我们从一个信念开始,称为先验。然后我们获取一些数据并使用它来更新我们的信念。结果称为后验。如果我们获得更多数据,旧的后验就会变成新的先验,循环重复。
此过程采用贝叶斯规则:
P( A | B ) = P( B | A ) * P( A ) / P( B )
P( A | B ),读作“A 的概率给定 B”,表示条件概率:如果 B 发生,A 的可能性有多大。
从数据推断模型参数
在贝叶斯机器学习中,我们使用贝叶斯规则从数据 (D) 推断模型参数 (theta):
P( theta | D ) = P( D | theta ) * P( theta ) / P( data )
这一切的组成部分都是概率分布。
P( data )是我们通常无法计算的东西,但由于它只是一个归一化常数,所以没有那么重要。在比较模型时,我们主要对包含 theta 的表达式感兴趣,因为P( data )每个模型都保持相同。
P( theta )是先验的,或者我们对模型参数可能是什么的信念。大多数情况下,我们对这个问题的看法相当模糊,如果我们有足够的数据,我们根本不在乎。只要它在先验中不为零,推理就应该收敛到可能的 theta。一个根据参数化分布指定先验- 请参阅先验从何而来。
P( D | theta )被称为给定模型参数的数据的似然性。似然公式是特定于模型的。人们经常使用似然来评估模型:对真实数据给出更高似然的模型更好。
最后,P( theta | D )后验,就是我们所追求的。它是从先验信念和数据获得的模型参数的概率分布。
当使用似然来获得模型参数的点估计时,它被称为最大似然估计或 MLE。如果还考虑了先验,那么它就是最大后验估计(MAP)。如果先验是一致的,则 MLE 和 MAP 相同。
请注意,选择模型可以与选择模型(超)参数分开。但在实践中,它们通常通过验证一起执行。
模型与推理
推理是指您如何学习模型的参数。模型与您的训练方式是分开的,尤其是在贝叶斯世界中。
考虑深度学习:您可以使用 Adam、RMSProp 或许多其他优化器来训练网络。然而,它们往往彼此相当相似,都是随机梯度下降的变体。相比之下,贝叶斯推理方法彼此之间的差异更大。
两种最重要的方法是蒙特卡罗采样和变分推理。采样是黄金标准,但速度很慢。The Master Algorithm的摘录有更多关于 MCMC 的内容。
变分推理是一种明确设计的方法,旨在以一定的准确性换取速度。它的缺点是它是特定于模型的,但隧道尽头有光明 - 请参阅下面的软件部分和变分推理:统计学家评论。
统计建模
在贝叶斯方法的范围内,有两种主要风格。我们将第一个统计建模和第二个概率机器学习称为。后者包含所谓的非参数方法。
当数据稀缺、珍贵且难以获得时,就会发生建模,例如在社会科学和其他难以进行大规模受控实验的环境中。想象一个统计学家使用他拥有的少量数据精心构建和调整模型。在此设置中,您不遗余力地充分利用可用输入。
此外,对于小数据,量化不确定性很重要,而这正是贝叶斯方法的擅长之处。
贝叶斯方法 - 特别是 MCMC - 通常计算成本很高。这再次与小数据密切相关。
要体验一下,请考虑使用回归分析和多级/分层模型进行数据分析一书的示例。那是一本关于线性模型的整本书。他们以一声巨响开始:一个没有预测变量的线性模型,然后通过一个预测变量、两个预测变量、六个预测变量、最多 11 个的线性模型。
这种劳动密集型模式违背了机器学习的当前趋势,即使用数据让计算机自动从中学习。
概率机器学习
让我们尝试用“概率”代替“贝叶斯”。从这个角度来看,它与其他方法没有太大区别。就分类而言,大多数分类器都能够输出概率预测。甚至 SVM,这是贝叶斯的对立面。
顺便说一下,这些概率只是来自分类器的信念陈述。它们是否对应于真实概率完全是另一回事,它被称为校准。
LDA,一个生成模型
潜在狄利克雷分配是一种方法,可以将数据抛出并允许它对事物进行分类(与手动建模相反)。它类似于矩阵分解模型,尤其是非负 MF。您从一个矩阵开始,其中行是文档,列是单词,每个元素是给定文档中给定单词的计数。LDA 将这个大小为nxd 的矩阵“分解”为两个矩阵,文档/主题(nxk)和主题/单词(kxd)。
与因式分解的不同之处在于您不能将这两个矩阵相乘以获得原始矩阵,但由于适当的行/列总和为 1,您可以“生成”一个文档。要获取第一个单词,先对主题进行采样,然后从该主题中抽取一个单词(第二个矩阵)。对您想要的多个单词重复此操作。请注意,这是一个词袋表示,而不是正确的词序列。
上面是一个生成模型的例子,这意味着可以从中采样或生成示例。与分类器进行比较,分类器通常P( y | x )基于x 进行建模以区分类别。生成模型涉及的联合分布Ÿ和X,P( y, x )。估计该分布更困难,但它允许采样,当然可以P( y | x )从P( y, x ).
贝叶斯非参数
虽然没有确切的定义,但该名称意味着模型中的参数数量会随着可用数据的增加而增加。这类似于支持向量机,例如,算法从训练点中选择支持向量。非参数包括 LDA 的分层狄利克雷过程版本,其中主题的数量自动选择,以及高斯过程。
高斯过程
高斯过程有点类似于支持向量机——两者都使用内核并且具有相似的可扩展性(多年来通过使用近似值得到了极大的改进)。GP 的一个自然公式是回归,分类是事后的想法。对于 SVM,情况正好相反。
另一个区别是 GP 从头开始是概率性的(提供误差线),而 SVM 不是。您可以在回归中观察到这一点。大多数“正常”方法仅提供点估计。贝叶斯对应物,如高斯过程,也输出不确定性估计。
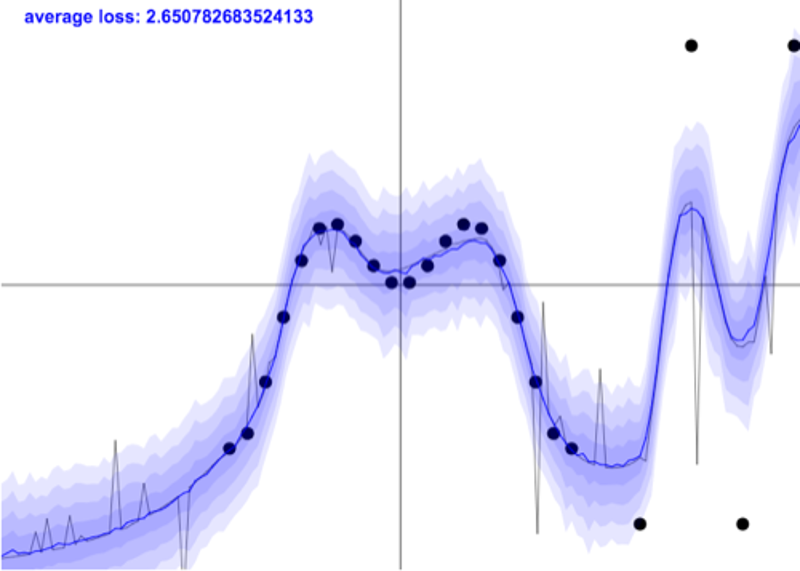
图片来源:Yarin Gal 的异方差 dropout 不确定性 和我的深层模型不知道的东西
不幸的是,这并不是故事的结局。即使是像 GP 这样的复杂方法,通常也是在同方差假设下运行的,即均匀的噪声水平。实际上,噪声在输入空间中可能不同(异方差) - 请参见下图。
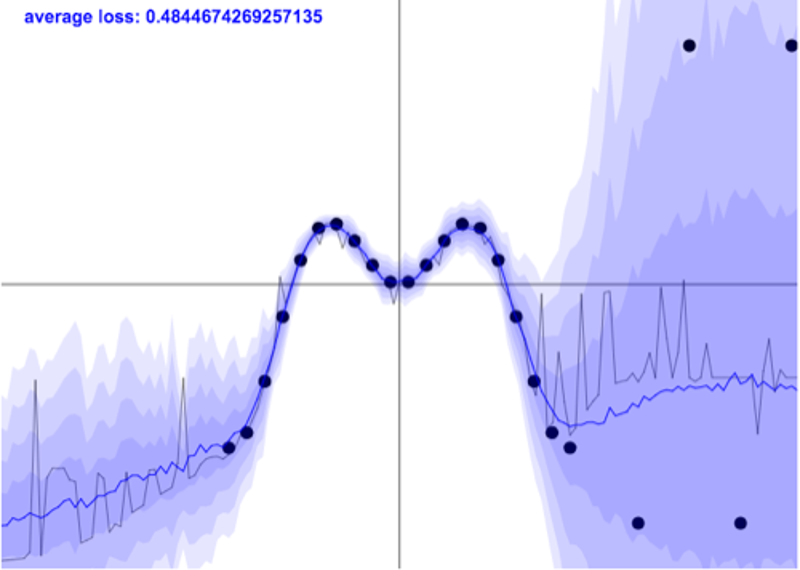
高斯过程的一个相对流行的应用是机器学习算法的超参数优化。数据很小,无论是在维度上 - 通常只有几个要调整的参数,而且在示例的数量上。每个示例代表目标算法的一次运行,这可能需要数小时或数天。因此,我们希望用尽可能少的例子来了解好东西。
大多数关于 GP 的研究似乎发生在欧洲。English 在使 GP 更易于使用方面做了一些有趣的工作,最终出现了自动统计员,这是一个由 Zoubin Ghahramani 领导的项目。
观看此视频的前 10 分钟,了解高斯过程的可访问介绍。
软件
当今最引人注目的贝叶斯软件可能是Stan。Stan 是一种概率编程语言,这意味着它允许您指定和训练您想要的任何贝叶斯模型。它在 Python、R 和其他语言中运行。Stan 有一个名为NUTS的现代采样器:
[在斯坦] 的大部分计算是使用哈密顿蒙特卡罗来完成的。HMC 需要进行一些调整,因此 Matt Hoffman 提出并编写了一个新算法 Nuts(“No-U-Turn Sampler”),它可以自适应地优化 HMC。在许多设置中,Nuts 实际上比最佳静态 HMC 的计算效率更高!
关于 Stan 的一件特别有趣的事情是它具有自动变分推理:
变分推理是一种用于近似贝叶斯推理的可扩展技术。导出变分推理算法需要繁琐的特定于模型的计算;这使得自动化变得困难。我们提出了一种自动变分推理算法,自动微分变分推理(ADVI)。用户只提供一个贝叶斯模型和一个数据集;没有其他的。
这项技术为将小型建模应用于至少中等规模的数据铺平了道路。
在 Python 中,最流行的包是PyMC。它没有那么先进或完善(开发人员似乎在追赶 Stan),但仍然不错。PyMC 有 NUTS 和 ADVI - 这是一个带有minibatch ADVI 示例的笔记本。该软件使用 Theano 作为后端,因此它比纯 Python 更快。
更新:Edward是一个建立在 TensorFlow 之上的概率编程库。它具有一些深度模型,并且似乎比竞争对手更快,至少在使用 GPU 时是这样。
Infer.NET是 Microsoft 的概率编程库。它主要可从 C# 和 F# 等语言中获得,但显然也可以从 .NET 的 IronPython 中调用。Infer.net默认使用期望传播。
除此之外,还有无数的包实现了各种风格的贝叶斯计算,从其他概率编程语言到专门的 LDA 实现。一个有趣的例子是CrossCat:
CrossCat 是一种域通用的贝叶斯方法,用于分析高维数据表。CrossCat 通过分层非参数贝叶斯模型中的近似推理,从数据中估计表中变量的完整联合分布,并为每个条件分布提供高效的采样器。CrossCat 结合了非参数混合建模和贝叶斯网络结构学习的优势:在给定足够数据的情况下,它可以通过设置潜在变量对任何联合分布进行建模,而且还可以发现可观察变量之间的独立性。
资源
为了巩固您的理解,您可以阅读 Radford Neal 的关于机器学习贝叶斯方法的教程。它对应于这篇文章的主题 1:1。
我们发现 Kruschke 的《做贝叶斯数据分析》,被称为幼书,可读性最高。作者不遗余力地解释建模的所有细节。
统计重新思考似乎是类似的,但更新。它在 R + Stan 中有示例。作者 Richard McElreath在 YouTube 上发表了一系列讲座。
在机器学习方面,这两本书都只涉及线性模型。同样,Cam Davidson-Pylon 的Probabilistic Programming & Bayesian Methods for Hackers涵盖了贝叶斯部分,但不包括机器学习部分。
Alex Etz 关于理解贝叶斯的系列文章也是如此。
对于那些喜欢数学的人来说,机器学习: Kevin Murphy的概率视角可能是一本值得一看的好书。你喜欢硬核?没问题,Bishop 的模式识别和机器学习可以帮助您解决问题。最近的一个Reddit 帖子简要讨论了这两个。
David Barber 的Bayesian Reasoning and Machine Learning也很受欢迎,并且可以在网上免费获得,关于这个问题的经典书籍Gaussian Processes for Machine Learning也是如此。
据我们所知,有贝叶斯学习机没有MOOC,但mathematicalmonk解释机器学习从贝叶斯观点。
注意:本文归作者所有,未经作者允许,不得转载

