来自 http://blog.163.com/zhoulili1987619@126/blog/static/353082012015516103746884/
指数平滑法对于预测涞水是非常有帮助的,而且它对时间序列上面连续的值之间相关性咩有要求。但是,如果你想使用指数平滑法计算出预测区间,那么预测误差必须是
不相关的,而且必须是服从零均值、方差不变的正态分布。即使指数平滑法对时间序列连续数值之间相关性没有要求,在某种情况下,我们可以通过考虑数据之间的相关性来创建更好的预测模型。
自回归移动平均模型(ARIMA)包含一个确定(explict)的统计模型用于处理时间序列的不规则部分,它也允许不规则部分可以自相关。
1)时间序列的差分
ARIMA模型为平稳时间序列定义的。因此,如果你从一个非平稳的时间序列开始,首先你就需要做时间序列差分直到你得到一个平稳时间序列。
如果你必须对时间序列做d阶差分才能得到一个平稳序列,那么你就使用ARIMA(p,d,q)模型,其中d是差分的阶数。
在R中你可以使用diff()函数作时间序列的差分。例如,每年女人裙子边缘的直径做成的时间序列数据,从1866年到1911年在平均值上是不平稳的。
加,数值变化很大。
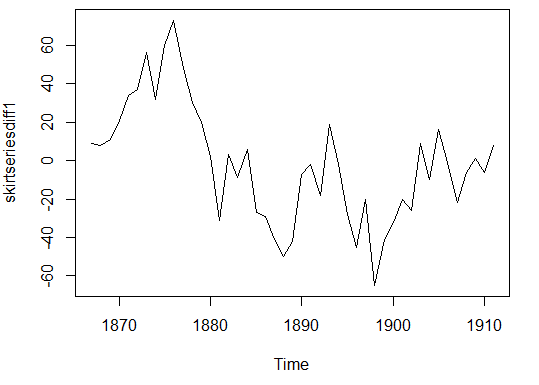
我们可以通过键入下面的代码来得到时间序列(数据存于“skirtseries”)的一阶差分,并画出差分序列的图:
> skirtseriesdiff1 <- diff(skirtseries,differences=1)
> plot.ts(skirtseriesdiff1)
一阶差分时间序列结果(上图)的均值看起来并不平稳。因此,我们需要再次做差分,来看一下是否能得到一个平稳时间序列:
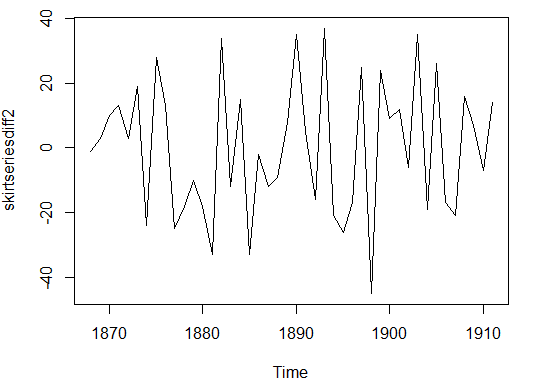
> skirtseriesdiff2 <- diff(skirtseries,differences=2)
> plot.ts(skirtseriesdiff2)
对于平稳性正式的检验
对于平稳性正式的检验称作“单位根测试”,可以在fUnitRoots包中得到。
二次差分(上面)后的时间序列在均值和方差上确实看起来像是平稳的,随着时间推移,时间序列的水平和方差大致保持不变。因此,看起来我们需要
对裙子直径进行两次差分以得到平稳序列。
如果你需要对你的原始时间序列数据做d阶差分来获得一个平稳时间序列,那么意味着你可以对你的时间序列使用ARIMA(p,d,q)模型,其中d是差分的阶数,例如,
对于女人裙子直径的时间序列,我们必须进行两次差分,所以差分的阶数就是2,这意味着你可以用ARIMA(p,2,q)模型。接下来我们需要找到ARIMA模型中的p值和q值。
另外一个事件序列的例子是英国(几位)国王依次去世年龄的时间序列
2)选择一个合适的ARIMA模型
如果你的时间序列是平稳的,或者你通过做n次差分转化为一个平稳时间序列,接下来就是要选择合适的ARIMA模型,这意味着需要寻找ARIMA(p,d,q)中合适的p值和q值。为了
得到这些,通常需要检查平稳时间序列的(自)相关图和偏相关图。
我们使用R中的”acf()”和”pacf”函数来分别(自)相关图和偏相关图。在”acf()”和”pacf”设定”plot=FALSE”来得到自相关和偏相关的真实值。
英国国王去世年龄的例子
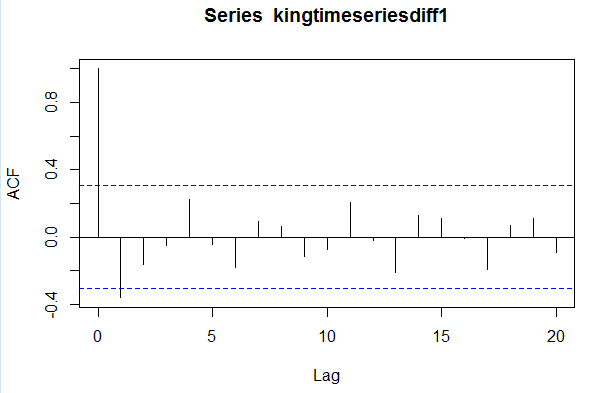
例如,要画出国王去世年龄一阶差分序列滞后1-20阶数(lags 1-20)的相关图,并且得到其自相关系数,我们输入:
> kingtimeseriesdiff1 <- diff(kingtimeseries,difference=1)
> acf(kingtimeseriesdiff1,lag.max=20)
> acf(kingtimeseriesdiff1,lag.max=20,plot=FALSE)
Autocorrelations of series ‘kingtimeseriesdiff1’, by lag
0 1 2 3 4 5 6 7 8 9 10
1.000 -0.360 -0.162 -0.050 0.227 -0.042 -0.181 0.095 0.064 -0.116 -0.071
11 12 13 14 15 16 17 18 19 20
0.206 -0.017 -0.212 0.130 0.114 -0.009 -0.192 0.072 0.113 -0.093
我们从上面相关图中可以看出在滞后1阶(lag1)的自相关值(-0.360)超出了置信边界,但是其他所有在滞后1-20阶(lags 1-20)的自相关值都没有超出置信边界。
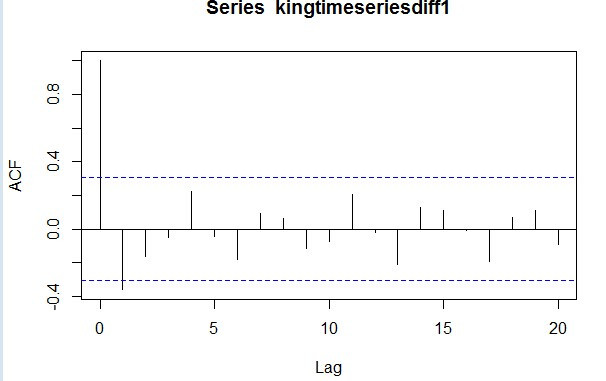
要画出英国国王去世年龄在滞后1-20阶(lags 1-20)一阶差分时间序列的偏相关图,并得到偏相关的值,我们使用“pcf()”函数,输入:
> pacf(kingtimeseriesdiff1,lag.max=20)
> pacf(kingtimeseriesdiff1,lag.max=20,plot=FALSE)
Partial autocorrelations of series ‘kingtimeseriesdiff1’, by lag
1 2 3 4 5 6 7 8 9 10 11
-0.360 -0.335 -0.321 0.005 0.025 -0.144 -0.022 -0.007 -0.143 -0.167 0.065
12 13 14 15 16 17 18 19 20
0.034 -0.161 0.036 0.066 0.081 -0.005 -0.027 -0.006 -0.037
偏相关图显示在滞后1,2和3阶(lags 1,2,3)时的偏自相关系数超出了置信边界,为负值,且在等级上随着滞后阶数的增加而缓慢减少
(lag 1:-0.360,lag 2:-0.335,lag 3:-0.321)。从lag 3之后偏自相关系数值缩小至0. 既然自相关值在滞后1阶(lag 1)之后为0,
且偏相关值在滞后3阶(lag 3)之后缩小至 0,那么意味着接下来的ARIMA(自回归移动平均)模型对于一阶时间序列有如下性质: .
ARMA(3,0)模型:即偏自相关值在滞后3阶(lag 3)之后缩小至0且自相关值缩小至0(即使此模型中说自相关值缩小至0有些不太合适),
则是一个阶层p=3自回归模型。
ARMA(0,1)模型:即自相关图在滞后1阶(lag 1)之后为0且偏自相关图缩小至0,则是一个阶数q=1的移动平均模型。
ARMA(p,q)模型:即自相关图和偏相关图都缩小至0(即使此模型中说自相关图缩小至0有些不太合适),则是一个具有p和q大于0的混合模型。
我们利用简单的原则来确定哪个模型是最好的:即我们认为具有最少参数的模型是最好的。ARMA(3,0)有3个参数,ARMA(0,1)有1个参数,
而ARMA(p,q)至少有2个变量。因此ARMA(0,1)模型被认为是做好的模型。 ARMA(0,1)模型是一阶的移动平均模型,或者称作MA(1)。
这个模型可以写作:X_t – mu = Z_t – (theta * Z_t-1),其中X_t是我们学习的平稳时间序列(英国国王去世年龄的一阶差分),
mu是时间序列X_t的平均值,Z_t是具有平均值为0且方差为常数的白噪音,thetathetathetathetatheta是可以被估计的参数。
是可以被估计的参数。
移动平均模型通常用于建模一个时间序列,此序列具有邻项观察值之间短期相关的特征。直观地,可以很好理解MA模型可以用来描
述英国国王去世年龄的时间序列中不规则的成分,比如我们可能期望某位英国国王的去世年龄对接下来的1或2个国王的去世年龄有某种影响,
而对更远之后的国王去世年龄没有太大的影响。
快捷方式:auto.arima() 函数
auto.arima() 函数可以用来发现合适的ARIMA模型,例如输入 “library(forecast)”, 然后 “auto.arima(kings)”. 那么输出说明合适的模型
是ARIMA(0,1,1). 既然对于英国国王去世年龄的时间序列,ARIMA(0,1)被认为是最合适的模型,那么原始的时间序列可以使用ARIMA(0,1,1)
(p=0,d=1,q=1,这里d是差分阶层所需要的)来建模。
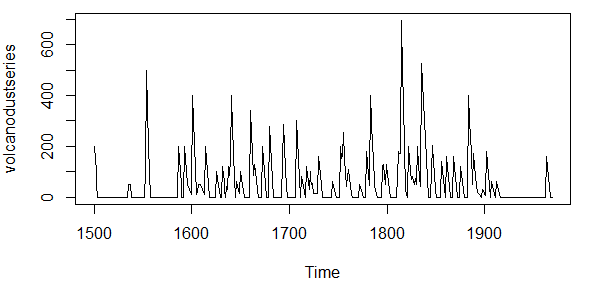
北半球的火山灰覆盖实例
> volcanodust <- scan(“D:\\test\\timeseries\\dvi.txt”,skip=1)
Read 470 items
> str(volcanodust)
num [1:470] 200 150 100 50 0 0 0 0 0 0 …
> volcanodustseries <- ts(volcanodust,start=c(1500))
> plot.ts(volcanodustseries)
从图上看出,随着时间增加,时间序列上面的随机波动逐渐趋与一个常数,所以添加一个合适的模型可以很好地描述这个时间序列。
进一步地,此时间序列看起来在平均值和方差上面是平稳的,即随着时间变化,他们的水平和方差大致趋于常量。因此,我们不需要
做差分来适应ARIMA模型,而是用原始数据就可以找到合适的ARIMA模型(序列进行差分还是需要的,d为0)。
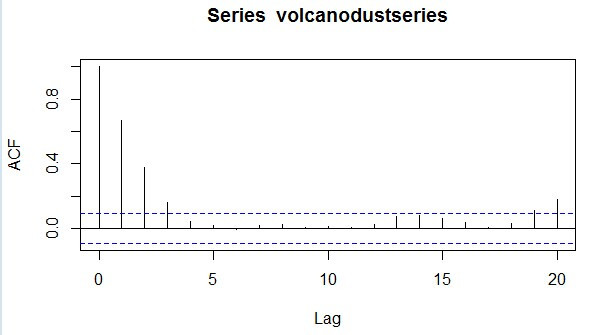
> acf(volcanodustseries,lag.max=20)
> acf(volcanodustseries,lag.max=20,plot=FALSE)
Autocorrelations of series ‘volcanodustseries’, by lag
0 1 2 3 4 5 6 7 8 9 10
1.000 0.666 0.374 0.162 0.046 0.017 -0.007 0.016 0.021 0.006 0.010
11 12 13 14 15 16 17 18 19 20
0.004 0.024 0.075 0.082 0.064 0.039 0.005 0.028 0.108 0.182
我们从相关图可以看到,自相关系数在滞后1,2和3阶(lags 1,2,3) 时超出了置信边界,且自相关值在滞后3阶(lag 3)之后缩小至0.
自相关值在滞后1,2,3阶(lags 1,2,3)上是正值, 且随着滞后阶数的增加而在水平上逐渐减少(lag 1: 0.666, lag 2: 0.374, lag 3: 0.162)。
自相关值在滞后19和20阶(lags 19,20)上也超出了显著(置信)边界,但既然它们刚刚超出置信边界(特别是lag19),那么很可能属于
偶然出现的,而自相关值在滞后4-18阶(lags 4-18)上都没有超出显著边界,而且我们可以期望1到20之间的会偶尔超出95%的置信边界。
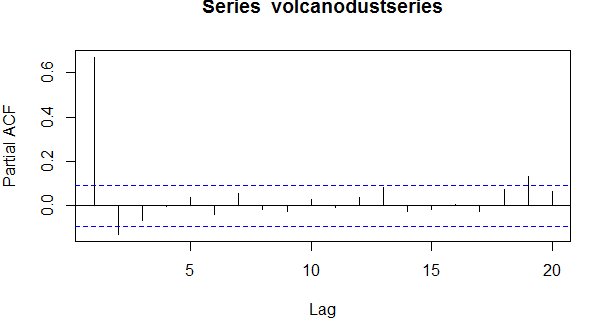
> pacf(volcanodustseries,lag.max=20)
> pacf(volcanodustseries,lag.max=20,plot=FALSE)
Partial autocorrelations of series ‘volcanodustseries’, by lag
1 2 3 4 5 6 7 8 9 10 11
0.666 -0.126 -0.064 -0.005 0.040 -0.039 0.058 -0.016 -0.025 0.028 -0.008
12 13 14 15 16 17 18 19 20
0.036 0.082 -0.025 -0.014 0.008 -0.025 0.073 0.131 0.063
从偏自相关图中我们看出在滞后1阶(lag 1)上偏自相关值(0.666)为正且超出了显著边界, 而在滞后2阶(lag 2)上面偏自相关值(-0.126)是
负的且也同样超出了置信边界。偏自相关值在滞后2阶(lag 2)之后缩小至0. 既然自相关图在滞后3阶(lag 3)之后缩小为0,且偏相关图在
滞后2阶(lag 2)之后缩小为0,那么下面的ARMA模型可能适合此时间序列:
ARMA(2,0) 模型,既然偏自相关图在滞后2阶(lag 2)之后缩小至0,且自相关图在滞后3阶(lag 3)之后缩小至0,且偏相关图在滞后2阶(lag 2)之后为0.
ARMA(0,3) 模型,既然自相关图在滞后3阶(lag 3)之后为0,且偏相关缩小至0 (尽管这点对于此模型不太合适)
ARMA(p,q) 混合模型, 既然自相关图和偏相关图都缩小至0 (尽管自相关图缩小太突然对这个模型不太合适)
Shortcut: the auto.arima() function快捷方式:auto.arima()函数
同样,我们可以使用auto.arima()来寻找合适的模型,通过输入“auto.arima(volcanodust)”, 给出ARIMA(1,0,2), 这里含有3个参数.
但是, 可以使用不同的标准来选择合适的模型(参见 auto.arima()的帮助页面)。如果你使用 “bic” 标准, 这里对参数个数要求非常严格,
我们可以得到ARIMA(2,0,0), 即ARMA(2,0): “auto.arima(volcanodust,ic=”bic”)”.
ARMA(2,0) 模型有2个参数, ARMA(0,3) 模型有3 个参数,而ARMA(p,q) 模型有至少2个参数。
因此,使用简单的原则, ARMA(2,0) 模型和ARMA(p,q) 模型在这里是同样优先的选择模型。
ARMA(2,0)是2阶的自回归模型,或者称作RA(2)模型。
此模型可以写作: X_t – mu = (Beta1 * (X_t-1 – mu)) + (Beta2 * (Xt-2 – mu)) + Z_t,
其中X_t 是我们学习的平稳时间序列(火山灰覆盖指数的时间序列),mu 是时间序列 X_t的平均值, Beta1 和Beta2 是估计的参数,
Z_t 是平均值为0且方差为常数的白噪音。 AR (autoregressive) 模型通常被用来建立一个时间序列模型,此序列在邻项观测值上具有长期相关性
直观地,AR 模型可以用描述火山灰覆盖指数的时间序列来很好地理解,如我们可以期望在某一年的火山灰水平将会影响到后面的很多年,既然火
山灰并不可能会迅速的消失。 如果ARMA(2,0) 模型(with p=2, q=0) 被用于建模火山灰覆盖指数的时间序列,它也将意味着ARIMA(2,0,0) 模型也
可以使用。(with p=2, d=0, q=0, 其中d是差分的阶数). 类似地,如果ARMA(p,q) 混合模型可以使用, 其中p和q的值均大于0, 那么ARIMA(p,0,q)
模型也可以使用。
3)使用ARIMA模型进行预测
一旦你为你的时间序列数据选择了最好的ARIMA(p,d,q) 模型,你可以估计ARIMA模型的参数,并使用它们做出预测模型来对你时间序列中的未
来值作预测。你可以使用R中的“arima()”函数来估计ARIMA(p,d,q)模型中的参数
例如,我们上面讨论的ARIMA(0,1,1) 模型看起来对英国国王去世年龄的时间序列是非常合适的模型。你可以使用R中的“arima()”函数的“order”
参数来确定ARIMA模型中的p,d,q值。为了对这个时间序列(它存放在 “kingstimeseries”变量中, 见上)使用合适的ARIMA(p,d,q) 模型,
我们输入:
> king <- scan(“D:\\test\\timeseries\\king.txt”,skip=3)
Read 42 items
> kingtimeseries <- ts(king)
> kingtimeseries
Time Series:
Start = 1
End = 42
Frequency = 1
[1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59
[25] 48 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56
> kingtimeseriesarima <- arima(kingtimeseries,order=c(0,1,1))
> kingtimeseriesarima
Call:
arima(x = kingtimeseries, order = c(0, 1, 1))
Coefficients:
ma1
-0.7218
s.e. 0.1208
sigma^2 estimated as 230.4: log likelihood = -170.06, aic = 344.13
上面提到,如果我们对时间序列使用ARIMA(0,1,1)模型,那就意味着我们对一阶时间序列使用了ARMA(0,1) 模型。
ARMA(0,1) 模型可以写作X_t – mu = Z_t – (theta * Z_t-1),其中theta是被估计的参数。 从R 中“arima()”函数的输入(上面),
在国王去世年龄的时间序列中使用ARIMA(0,1,1) 模型的情况下,theta 的估计值(在R输出中以‘ma1’给出) 为-0.7218。
4)指定预测区间的置信水平
你可以使用forecast.Arima() 中“level”参数来确定预测区间的置信水平。例如,为了得到99.5%的预测区间,我们输入:
“forecast.Arima(kingstimeseriesarima, h=5, level=c(99.5))”. 然后我们可以使用ARIMA模型来预测时间序列未来的值,
使用R中forecast包的“forecast.Arima()” 函数。例如,为了预测接下来5个英国国王的去世年龄,我们输入:
> library(forecast)
> kingtimeseriesforecast <- forecast.Arima(kingtimeseriesarima,h=5)
> kingtimeseriesforecast
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
43 67.75063 48.29647 87.20479 37.99806 97.50319
44 67.75063 47.55748 87.94377 36.86788 98.63338
45 67.75063 46.84460 88.65665 35.77762 99.72363
46 67.75063 46.15524 89.34601 34.72333 100.77792
47 67.75063 45.48722 90.01404 33.70168 101.79958
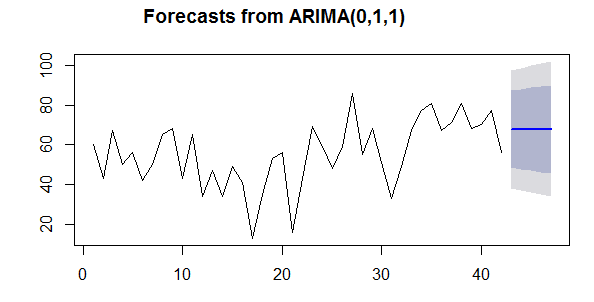
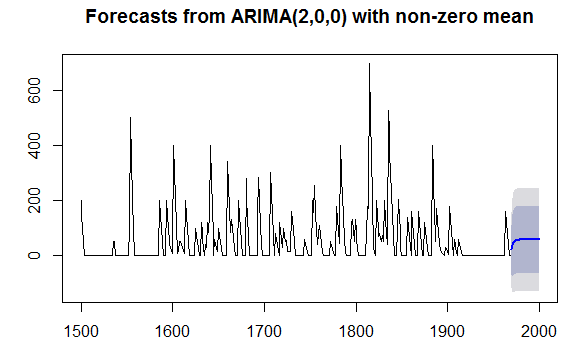
原始时间序列中包括42位英国国王的去世年龄。forecast.Arima()函数给出接下去5个国王(国王43-47)去世年龄的预测,对于这
些预测的预测区间我们同时设置为80%和95% 。第42位英国国王的去世年龄是56岁(在我们时间序列中的最后一位观察值),,ARIMA模型
给出接下来5位国王的预测去世年龄为67.8岁。 我们可以画出42位国王去世年龄的观察值,同样画出使用ARIMA(0,1,1)模型得到的42位
国王的预测去世年龄和接下去5位国王的预测值,输入:
> plot.forecast(kingtimeseriesforecast)
在指数平滑模型下,观察ARIMA模型的预测误差是否是平均值为0且方差为常数的正态分布(服从零均值、方差不变的正态分布)是个好主意,
同时也要观察连续预测误差是否(自)相关。 例如,我们可以对国王去世年龄使用ARIMA(0,1,1)模型后所产生的预测误差做(自)相关图,
做LjungLjungLjungLjungLjung-BoxBoxBox检 验, 输入:
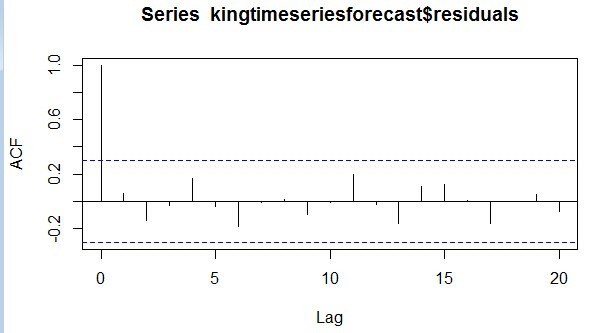
> acf(kingtimeseriesforecast$residuals,lag.max=20)
> Box.test(kingtimeseriesforecast$residuals,lag=20,type=”Ljung-Box”)
Box-Ljung test
data: kingtimeseriesforecast$residuals
X-squared = 13.584, df = 20, p-value = 0.8509
既然相关图显示出在滞后1-20阶(lags 1-20)中样本自相关值都没有超出显著(置信)边界,而且Ljung-Box检验的p值为0.9,所以我们推断在
滞后1-20阶(lags 1-20)中没有明显证据说明预测误差是非零自相关的。 为了调查预测误差是否是平均值为零且方差为常数的正态分布(服从
零均值、方差不变的正态分布),我们可以做预测误差的时间曲线图和直方图(具有正态分布曲线):
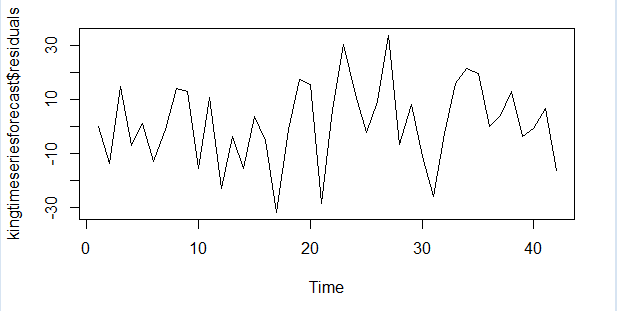
> plot.ts(kingtimeseriesforecast$residuals)
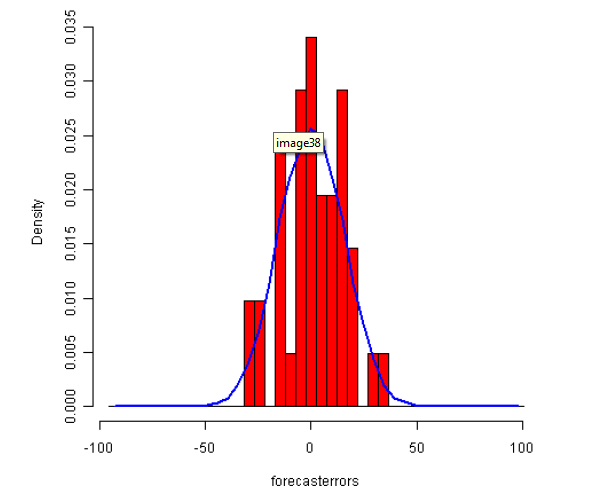
> plotForecastErrors(kingtimeseriesforecast$residuals)
示例(中的)预测中的时间曲线图显示出对着时间增加,方差大致为常数(大致不变)(尽管下半部分的时间序列方差看起来稍微高一些)。时间
直方图显示预测误大致是正态分布的且平均值接近于0(服从零均值的正态分布的)。因此,把预测误差看作平均值为0方差为常数正态分布(服从零
均值、方差不变的正态分布)是合理的。 既然依次连续的预测误差看起来不是相关,而且看起来是平均值为0方差为常数的正态分布(服从零均值、
方差不变的正态分布),那么对于英国国王去世年龄的数据,ARIMA(0,1,1)看起来是可以提供非常合适预测的模型。
5)北半球的火山灰覆盖问题
我们上面讨论了,处理火山灰覆盖的时间序列数据最合适的模型可能就是ARIMA(2,0,0)。为了使用ARIMA(2,0,0)来处理这个时间序列,
我们输入:
> volcanodustseriesarima <- arima(volcanodustseries, order=c(2,0,0))
> volcanodustseriesarima
Call:
arima(x = volcanodustseries, order = c(2, 0, 0))
Coefficients:
ar1 ar2 intercept
0.7533 -0.1268 57.5274
s.e. 0.0457 0.0458 8.5958
sigma^2 estimated as 4870: log likelihood = -2662.54, aic = 5333.09
如上所述,ARIMA(2,0,0)模型可以写作: X_t – mu = (Beta1 * (X_t-1 – mu)) + (Beta2 * (Xt-2 – mu)) + Z_t,,
这里Beta1和Beta2是估计参数。arima()函数的输出告诉我们这里Betal和Beta2估计值为 0.7533和-0.1268(由arima()输出中的ar1和ar2分别给出)。
现在我们要使用ARIMA(2,0,0) 模型, 我们可以用“forecast.ARIMA()” 模型来预测火山灰覆盖的未来。原始数据包含了1500至1969年间的数据。
为了预测1970年至2000年的数据,我们输入:
> volcanodustseriesforecasts <- forecast.Arima(volcanodustseriesarima, h=31)
> volcanodustseriesforecasts
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
1970 21.48131 -67.94860 110.9112 -115.2899 158.2526
1971 37.66419 -74.30305 149.6314 -133.5749 208.9033
1972 47.13261 -71.57070 165.8359 -134.4084 228.6737
1973 52.21432 -68.35951 172.7881 -132.1874 236.6161
1974 54.84241 -66.22681 175.9116 -130.3170 240.0018
1975 56.17814 -65.01872 177.3750 -129.1765 241.5327
1976 56.85128 -64.37798 178.0805 -128.5529 242.2554
1977 57.18907 -64.04834 178.4265 -128.2276 242.6057
1978 57.35822 -63.88124 178.5977 -128.0615 242.7780
1979 57.44283 -63.79714 178.6828 -127.9777 242.8634
1980 57.48513 -63.75497 178.7252 -127.9356 242.9059
1981 57.50627 -63.73386 178.7464 -127.9145 242.9271
1982 57.51684 -63.72330 178.7570 -127.9040 242.9376
1983 57.52212 -63.71802 178.7623 -127.8987 242.9429
1984 57.52476 -63.71538 178.7649 -127.8960 242.9456
1985 57.52607 -63.71407 178.7662 -127.8947 242.9469
1986 57.52673 -63.71341 178.7669 -127.8941 242.9475
1987 57.52706 -63.71308 178.7672 -127.8937 242.9479
1988 57.52723 -63.71291 178.7674 -127.8936 242.9480
1989 57.52731 -63.71283 178.7674 -127.8935 242.9481
1990 57.52735 -63.71279 178.7675 -127.8934 242.9481
1991 57.52737 -63.71277 178.7675 -127.8934 242.9482
1992 57.52738 -63.71276 178.7675 -127.8934 242.9482
1993 57.52739 -63.71275 178.7675 -127.8934 242.9482
1994 57.52739 -63.71275 178.7675 -127.8934 242.9482
1995 57.52739 -63.71275 178.7675 -127.8934 242.9482
1996 57.52739 -63.71275 178.7675 -127.8934 242.9482
1997 57.52739 -63.71275 178.7675 -127.8934 242.9482
1998 57.52739 -63.71275 178.7675 -127.8934 242.9482
1999 57.52739 -63.71275 178.7675 -127.8934 242.9482
2000 57.52739 -63.71275 178.7675 -127.8934 242.9482
我们可以画出原始时间序列和预测数值,输入:
> plot.forecast(volcanodustseriesforecasts)
一个棘手的问题这个模型预测中火山灰覆盖数据有负值,但是这个值只有正值才有意义。出现负值的原因是arima()和forecast.Arima()函数并知
道这个数值必须是正的。明显地,我们现在的预测模型中有并不令人满意的一面。
我们应该再次观察预测误差是否相关,且他们是否是平均值为0方差为常数的正态分布(服从零均值、方差不变的正态分布)。为了检测
相邻预测误差之间的相关性,我们做出相关图并使用Ljung-Box检验:
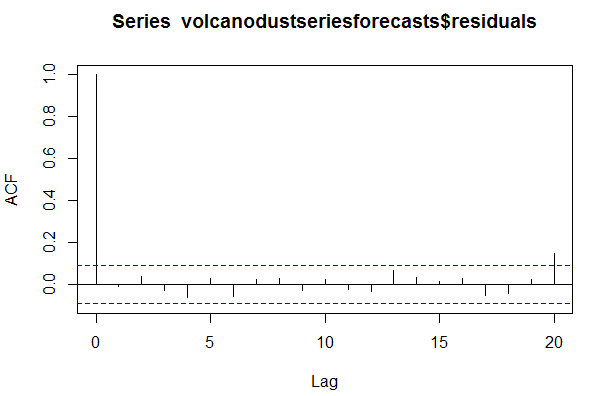
> acf(volcanodustseriesforecasts$residuals, lag.max=20)
> Box.test(volcanodustseriesforecasts$residuals, lag=20, type=”Ljung-Box”)
Box-Ljung test
data: volcanodustseriesforecasts$residuals
X-squared = 24.364, df = 20, p-value = 0.2268
相关图显示出示例在滞后20阶(lag 20)自相关值超出了显著(置信)边界。但是,这很可能是偶然的,既然我们认为1/20的样本自相关值是可以
超出95%显著边界的。另外,Ljung-Box检验的p值为0.2,表明没有证据证明在滞后1-20阶(lags 1-20)中预测误差是非零自相关的。 为了检查预
测误差是否是平均值为0且方差为常数的正态分布,我们做一个预测误差的时间曲线图和一个直方图:
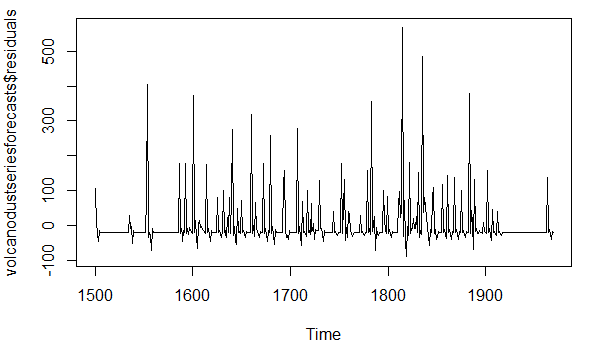
> plot.ts(volcanodustseriesforecasts$residuals)
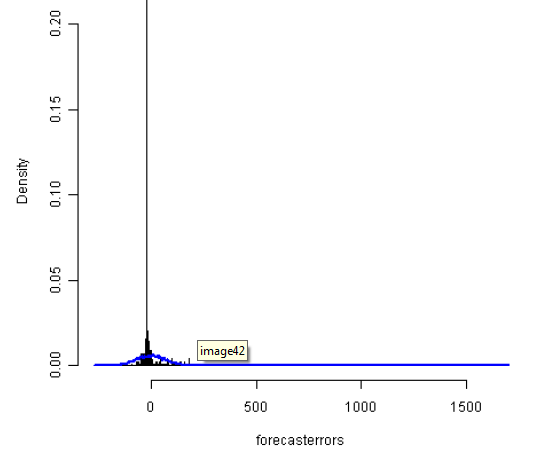
> plotForecastErrors(volcanodustseriesforecasts$residuals)
预测误差的时间曲线图显示随着时间推移预测误差的方差大致是常数,但是,预测误差的时间序列看起来有一个负值,而不是0. 通过计算预测误差
的平均我们可以确定其值为-0.22.
> mean(volcanodustseriesforecasts$residuals)
-0.2205417
预测误差的直方图(上图)显示尽管预测误差的平均值为负,与正态分布相比,预测误差的分布是向左偏移的。因此,我们推断说它是平均值为0且
方差为常数的正态分布是不太准确的。因此,ARIMA(2,0,0)很可能对火山灰覆盖时间序列数据来说并非是最好的模型,显然它是可以被优化的。
相关的链接阅读
对于R中深层的介绍,我们可以找到一个很好的在线引导资料在 “Kickstarting R”网站,
http://cran.r-project.org/doc/contrib/Lemon-kickstart/
这里有另外更深层的R的指导在“Introduction to R”网站, cran.r-project.org/doc/manuals/R-intro.html.
你可以在此找到一个R包的清单用于时间序列分析 CRAN Time Series Task View webpage.
如果要学习时间序列分析,我非常想推荐一本书“Time series” (product code M249/02) 由开放大学提供,可以在此找到the Open University Shop.
在 “Use R!” 系列中有两本书可以做时间序列分析,第一本是 Introductory Time Series with R 由 Cowpertwait和Metcalfe编写,另外一个是 Analysis of Integrated and Cointegrated Time Series with R 由Pfaff编写。
原创文章,作者:xsmile,如若转载,请注明出处:http://www.17bigdata.com/%e6%97%b6%e9%97%b4%e5%ba%8f%e5%88%97%e5%88%86%e6%9e%90-arima%e6%a8%a1%e5%9e%8b/
更多内容请访问:IT源点
注意:本文归作者所有,未经作者允许,不得转载